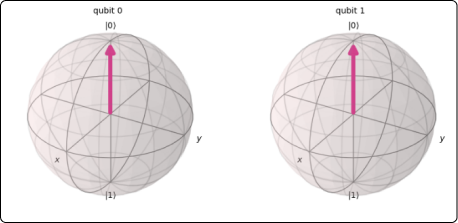
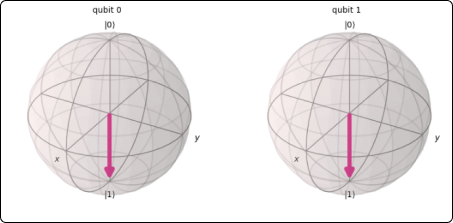
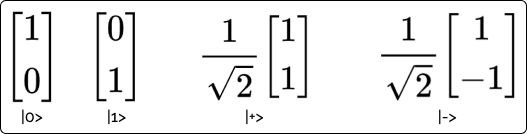Quantum Circuits
What is a quantum circuit?
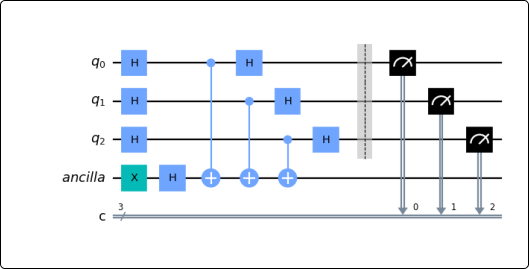
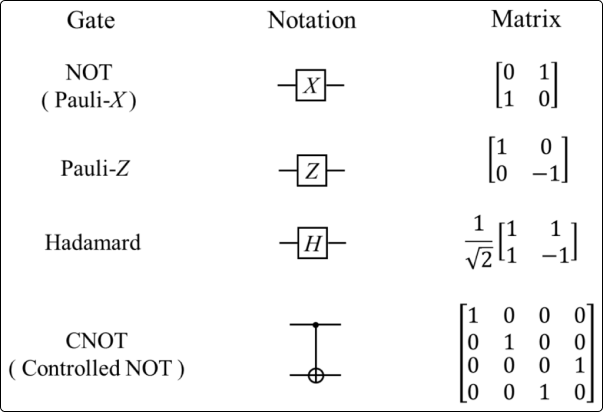
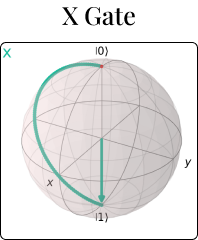
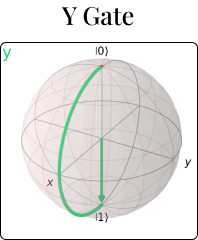
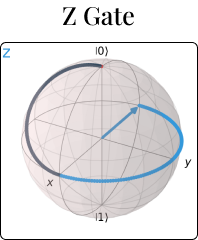
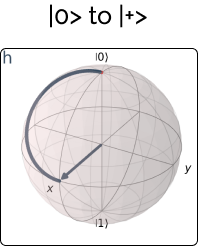
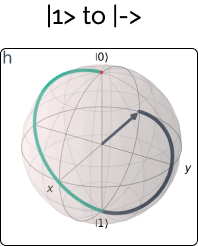
A quantum circuit is a sequence of operations on one or more qubits. Similar to classical circuits, the operations are represented using gates, quantum gates. The most popular quantum gates include the Hadamard Gate, Pauli Gates and the CNOT Gate.