Welcome to this section, where we will learn about three famous quantum algorithms by delving into how they could apply to some real life cases.
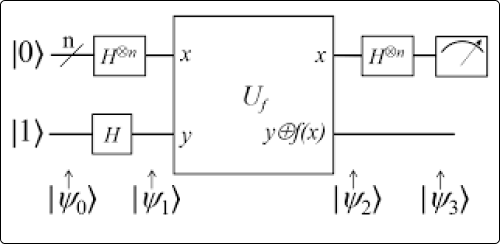
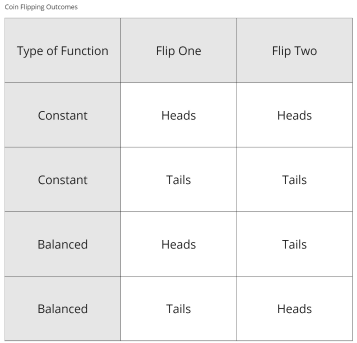
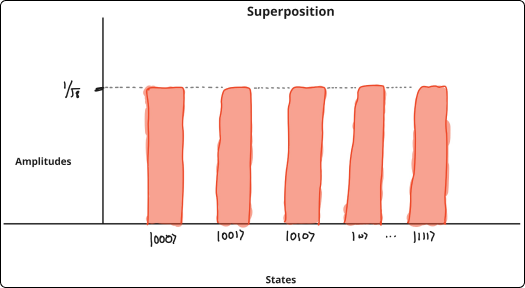
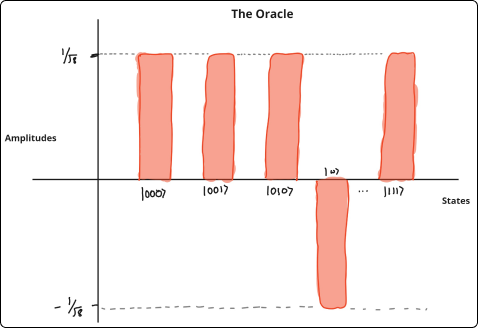
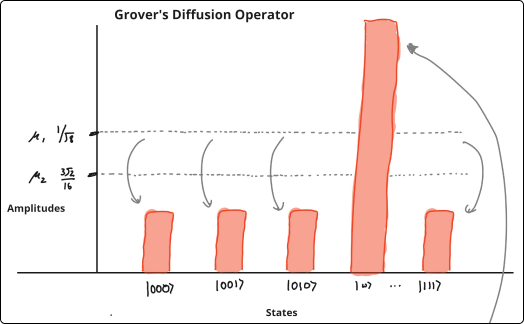
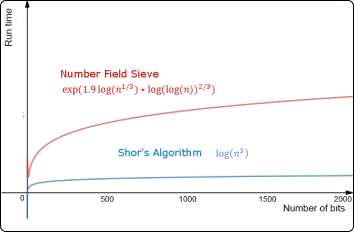
Say you have a coin, and you want to see if it's biased or not. In this hypothetical situation, the coin flip outcomes are strictly probabilistic; if biased, you would get the same outcome twice; otherwise, you would get different outcomes.
The table shows you would have four different scenarios based on two flips. You could get HH or TT, both of which indicate that the coin is biased, or you could get either HT or TH, which would suggest that the coin is fair.
Thinking classically, how could you determine whether the coin is fair? You must figure it out via brute force and flip it twice. Is there another better way to figure this out?
Well, by harnessing the power of quantum computers, you can. We can use a circuit like the one above. So imagine this: you are in a parallel universe, and you can simultaneously stimulate both coin flips. Then you can compare if the results are identical or different.
Quantumly, you would first put all the outcomes into superposition by applying a Hadamard gate. Then you would compare the two outcomes; if they are similar, you would get the result zero; however, if they aren't, you would get one. Sounds simple? Well, yes, that was the very first quantum algorithm. As time progressed, so did the algorithms; you will build on what you learned today in the following examples.
Finally, say you wanted to generalise from coin-flipping to other useful operations. A general use case for this algorithm would be anything that included a function, and you could test if the function was constant or biased.
If you wish to learn more about the algorithm, albeit more mathematically, watch this brilliant video by Artur Ekert. He includes details about oracles that we will use in the following examples.
You have a picture, and you want to find Wally. How would you go about finding Wally using a computer? Well, you would have to look at each character and compare it to the characteristics of Wally, and if it matches, you have found Wally, and if not, you keep going.
This method would take O(n) operations given that there are n characters. However, is there a faster way you could do this? Yes, there is! See Grover's Algorithm Circuit, which does it in O(n^1/2) or O(square root n) steps. A quadratic speedup!
At a high level, what we need to do, is to visualise every possible character at the same time; then, for the characters that share characteristics with Wally, we increase the probability of measuring it, and then for the ones that don't, we decrease the chance of measuring it. If we repeat this process root n times, we should have a very high (almost certain) probability of measuring Wally.
Let's go into more detail now.
In this scenario, there are only eight characters. The first step is assigning each character a state to simulate all the states simultaneously. And since three qubits allow for eight states, we only need to use three qubits. To demonstrate this, character one will have the state 000, character two 001 and so on, until character eight has 111. We must apply a Hadamard gate to each of the three qubits to visualise all the states simultaneously.
The second stage is Amplitude Amplification, a process that increases the amplitude of one state while reducing the amplitude of all the other states in the superposition. In this algorithm, amplitude amplification is created by an oracle and Grover's operator combined.
To visualise this, here's a diagram that shows all the states after putting them into equal superposition. They all have the same probability of being Wally. Note that Wally is at the state w.
Now we will see what the oracle and Grover's operator do to the superposition. The oracle is encoded with the characteristics of Wally. For instance. a red and white striped shirt, jeans and a cane. It will compare all the states simultaneously, but when a state matches the characteristics, it will change the amplitude of the state to a minus—essentially flagging it.
Secondly, Grover's operator looks for the mean amplitude and rotates each state about the mean. So all the states apart from the flagged one would decrease. Since there is such a significant disparity between Wally's state and the mean, the new amplitude of the state would be huge.
This process will repeat for approximately root n times, and then you can measure out Wally with a high probability!
Imagine you have a secret message locked using RSA encryption, which relies on the difficulty of factoring large numbers into prime factors. Breaking this encryption requires finding the two prime numbers multiplied to create the encryption key.
If we used a classical computer to break the RSA encryption, we would have to try many possible combinations of prime factors until we find the correct ones. This process would take a long time and require a lot of computational power.
The fastest way to currently do this would be using the Number Field Sieve Algorithm
However, Shor's powerful quantum algorithm offers a much faster approach to factorising large numbers. Here's how it works:
Shor's algorithm starts by utilising the power of quantum superposition. It allows us to consider multiple possible combinations of prime factors simultaneously.
Shor's algorithm applies a mathematical operation called the Quantum Fourier Transform (QFT) to analyse the combinations of prime factors. This operation enables the quantum computer to identify patterns in the factors.
Shor's algorithm uses quantum phase estimation to measure the periods or patterns of certain mathematical functions related to the factors. These periods contain information about the prime factors themselves.
The measurement then collapses the superposition into a specific set of factors, the prime numbers we sought.
Once the prime factors are obtained, we can break the RSA encryption and access the secret message.
Sounds complicated? Well, it was for me when I first learned about it. This video by minutephysics helped me to understand the algorithm quite well